Veamos un caso, con un límite infinito en la siguiente función:
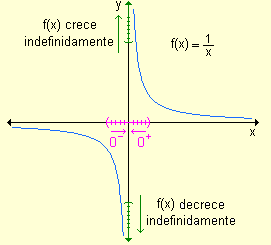
- si x ® 0+ los valores de la función crecen indefinidamente.
- si x ® 0- los valores de la función decrecen indefinidamente
- Las dos ramas de la curva se acercan cada vez más al eje y a medida que x se aproxima a cero. Para esta gráfica la recta x = 0 es asíntota vertical.
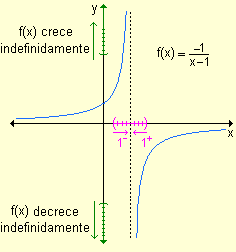
- si x ® 1+ los valores de la función decrecen indefinidamente.
- si x ® 1- los valores de la función crecen indefinidamente.
- Para esta gráfica la recta x = 1 es asíntota vertical.
- Las dos ramas de la curva se acercan cada vez más a la recta x = 1 a medida que x se aproxima a ese valor.
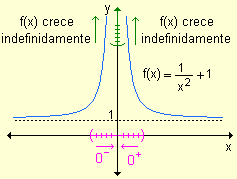
- si x ® 0+ los valores de la función crecen indefinidamente.
- si x ® 0- los valores de la función crecen indefinidamente.
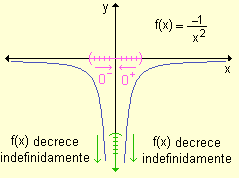
- si x ® 0+ los valores de la función decrecen indefinidamente.
- si x ® 0- los valores de la función decrecen indefinidamente.
- El comportamiento de estas funciones no puede describirse con la idea y el concepto de límite que se ha estudiado hasta ahora.Analizando nuevamente la función y =
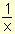 , se observa en la gráfica que cuando x ® 0+, los valores de f crecen más allá de todo tope. Por lo tanto f no tiene límite cuando x ® 0+. Sin embargo resulta conveniente decir que f(x) se aproxima a ¥ cuando x ® 0+. Se escribe.
, se observa en la gráfica que cuando x ® 0+, los valores de f crecen más allá de todo tope. Por lo tanto f no tiene límite cuando x ® 0+. Sin embargo resulta conveniente decir que f(x) se aproxima a ¥ cuando x ® 0+. Se escribe. 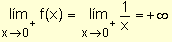 .
. - Esto no significa que el límite existe ni que +¥ es un número real, sino que expresa que la función se hace tan grande como deseamos escogiendo x suficientemente cercano a cero.
Ejemplo. Sea la gráfica de la función f(x) = 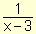 :
:
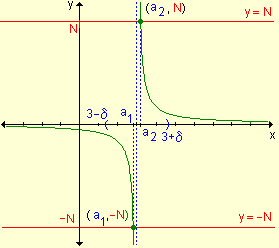

Observando la gráfica se puede escribir: 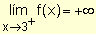 y
y 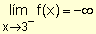
Para una mayor claridad te invito a observar el siguiente vídeo
LIMITES AL INFINITO






0 comentarios:
Publicar un comentario